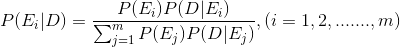통계학 홍찬식

Posted by doomsheart

Chap.01 서론

통계학은 자료를 수집하여 분석함으로써 자료가 가진 정보를 올바르게 해석할 수 있도록 해 주는 학문이다. 부분을 보고 전체에 대한 추론을 하는 것이 바로 통계학이다. 부분을 보고 전체에 대해 행하는 추론은 확률적 명제가 될 수밖에 없다.

1.1 기술통계학과 추론통계학

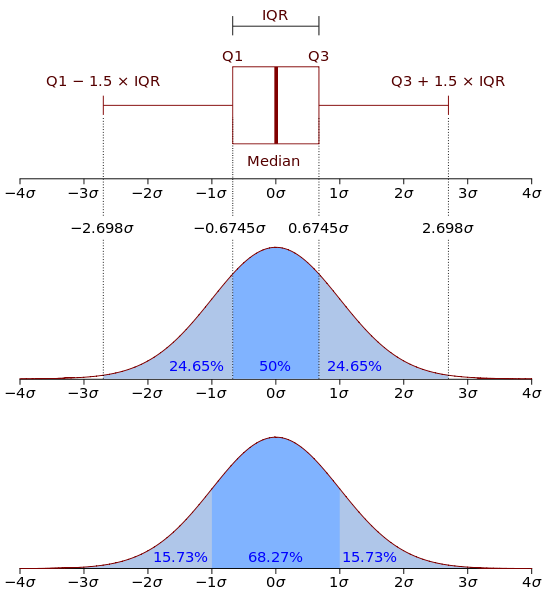
  • 기술통계학(descriptive statistics): 수집된 자료를 이해하기 쉽도록 요약하여 기술하는 것. 사분위범위 활용.
  • 추론통계학(inferential statistics): 일부만 관측한 자료를 효율적으로 이용하여 전체에 대해 추론하는 것.

1.2 모집단과 표본

  • 모집단(population): 관심의 대상인 집단 전체
  • 표본(sample): 모집단의 부분집합
  • 모수(parameter): 모집단의 특성을 나타내는 값. 미지의 고정된 상수(unknown but fixed constant), 표본이 어떻게 추출되든 모수의 값이 변하지 않음.
  • 통계량(statistic): 표본의 특성을 나타내는 값. 표본추출에 따른 변동을 보이는 확률변수(random variable)
  • 표본오차(sampling error): 통계량과 모수의 차이. 발생원인->대개 우연. 표본크기가 커질수록 오차 낮아짐. 반례)
  • 비표본오차(nonsampling error), 편의(bias):모집단을 잘 대표하지 못하는 표본추출.

1.3 실험계획과 표본조사

  • 실험계획: 어떤요인이 연구자가 관심을 가진 변수에 미치는 영향을 알아볼때 이용. 다른 요인의 영향을 통제하는 것이 중요
  • 표본조사: 통제된 실험이 불가능한 분야. 모집단을 잘 대표하는 표본을 추출.
  • 표본추출 방법:
    1. 무작위추출법(simple random sampling): 모집단에 속하는 모든 원소들이 표본에 포함될 가능성이 동일하도록 표본을 추출하는 방법.
    2. 계통추출법(systematic sampling): 첫 번째 원소를 무작위로 추출후 매번 k번째 요소를 표본으로 삼는것. (k, t+k, 2t+k, 3t+k….)
    3. 층화추출법(stratified sampling): 매우 이질적인 모집단을 층(stratum)이라 부르는 몇 개의 집단으로 구분하고 각 층에 일정한 표본 수를 할당한 다음 층별로 단순무작위표본을 추출하는 것. 하나의 층 내의 원소들이 가능한 한 동질적이어야 하는것이 중요. -> 적은 수의 표본으로도 그 층의 특성을 잘 파악 가능.
    4. 집락추출법(cluster sampling): 모집단을 집락(cluster)이라 부르는 집단으로 구분하고 일정수의 집락을 무작위로 추출한 다음 선택된 집락에서 단순 무작위표본을 추출하는 방법. (층화추출법과의 차이?) :집락내의 원소들이 이질적일때 효율적. 단순 무작위추출법이나 중화추출법에 비해 많은 수의 표본은 요구. 그러나 빠른 시간내에 관측가능.

1.4 회귀분석

  • 회귀분석(regression analysis): 이론이 현실을 잘 설명하는지 실증적으로 분석하기 위해 두 변수사이의 관계를 통계자료를 이용하여 파악하는 통계기법.
  • 단순선형회귀모형: 독립변수와 종속변수라 부르는 오직 두 개의 변수만을 고려.
  • 다중선형회귀모형: 하나의 종속변수를 둘 이상의 독립변수로 설명하는 모형.

Chap.02 자료의 요약과 중요한 기술통계량들

2.1 도수분포와 히스토그램

  • 도수(frequency)

  • 도수분포(frequency distribution): 자료를 몇 개의 계급구간으로 나눈 다음 각 구간에 속하는 항목의 수를 표로 만든 것.

    • 자료

      data

    • 도수 분표

계급구간 도수
0~5 8
6~10 9
11~15 4
16~20 3
21~25 1
합 25
  • 상대도수(relative frequency): 도수를 항목의 총수로 나눈 값. 이것으로 표를 만든게 도수 분포표.
  • 히스토그램(histogram): 위를 그래프로 그린 것.
  • 누적도수분포(cumulative frequency distribution), 누적상대도수분포(cumulative relative frequency distribution)

2.2 자료의 위치를 나타내는 통계량

  • 평균(average, mean): 자료의 중심위치를 파악.
  • 중위수(median): 자료를 크기 순으로 정리 할 때 중간에 위치하는 값. 홀수=(n+1/2)번, 짝수=n/2번과 n+1/2번의 평균.
  • 최빈값(mode): 관측된 도구가 가장 많은 값.

  • 그외 백분위수(percentile), 십분위수(decile), 사분위수(quartile)

    quatile

2.3 자료의 변동성을 나타내는 통계량

  • 분산(variance): 자료의 변동성을 측정하기 위해 사용되는 것.

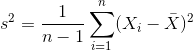
    variance

  • 자유도(degree of freedom): 관측치의 수에서 1을 뺀 n-1, 1뺀 이유는 8장에서 공부
    • Ex) a는 넓은범위 흩어져 있고 b는 평균주변에 밀집 -> 변동성 a > b, 분산 a > b
  • 표준편차(standard deviation): 분산의 제곱근, 변동성에 비례
  • 평균, 분산, 표준편차 모두 평균에 먼 값, 즉 이상치(outlier)에 의해 영향을 받음
  • 사분위 범위(IQR, interquartile range): IQR

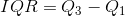
2.4 도수분포형태의 자료

2.5 산포도와 상관계수

  • 산포도(scatter diagram): 하나의 변수를 횡축에, 그리고 다른 하나의 변수를 종축에 측정 후 각 표본점을 좌표평면 상의 점으로 나타낸 것
  • 공분산(covariance):
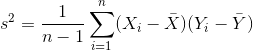
    covariance
    • 공분산은 부호만 의미가 있을 뿐 크기는 아무런 의미를 가지지 못함
  • 상관계수(correlation coefficient):
    • 측정단위에 따라 크기가 변하는 공분산의 단점을 보완.
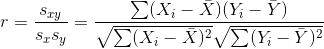
    • correlation coefficient
    • -1과 1사이의 값을 가짐. -1/1에 가까울수록 밀접한 음/양의 상관관계
  • 퀴즈는 이 링크에 jupyter-notebook으로 정리하였습니다.

Chap.03 사건과 확률

3.1 표본공간과 사건

  • 확률실험(random experiment) : 결과를 정확하게 예측할 수 없는 실험. 무작위 추출에 이용.
  • 표본공간(sample space) : S 또는 Ω로 표기. 확률실험에서 나타날 수 있는 모든 결과들을 모아놓은 집합.
  • 표본점(sample point) : 표본공간의 원소.
  • 사건(event) : 표본공간의 부분집합.
  • 상호배반(mutually exclusive) : 한 표본공간 내의 두 사건 A와 B가 동시에 발생할 수 없을 때. A∩B = Φ

3.2 확률과 확률공리

  • 확률공리 : 확률이 만족해야 할 조건을 약속해 놓은 것.
    • (1) 모든 사건 A에 대해 0 ≤ P(A) ≤ 1 이다.
    • (2) P(S) = 1 이고, P(Φ) = 0 이다.
    • (3) 두 사건 A와 B가 상호배반이면 P(A∪B) = P(A) + P(B)
  • 하나의 사건이 일어날 확률을 구하는 방법
    • (1) 고전적 방법 :
      • 1 / 가능한 모든 결과의 수
    • (2) 상대도수법 :
      • 일반적으로 유사한 조건하에서 관측된 사건발생의 상대도수를 그 사건의 확률로 보는 것.
    • (3) 주관적 확률:
      • 위 두개의 방법은 객관적 확률(누가 계산하여도 동일한 값을 가짐)인 반면, 실험의 결과들이 동일한 발생가능성을 가지고 있지도 않고 상대도수 자료도 구할 수 없을때 자신이 가진 모든 정보를 종합하여 사건의 발생 가능성에 대한 믿음의 정도를 0과 1사이의 숫자로 나타낸 것.

3.3 확률의 덧셈법칙

  • sum_of_probability
  • A ⊂ B 이면 P(A) ≤ P(B)
  • P(A∪B) = P(A) + P(B) - P(A∩B)

3.4 조건부확률과 통계적 독립

  • 조건부확률 : P(A|B) = 사건 B가 발생하였을때 사건 A가 일어날 확률.

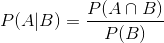
    conditional_probability

  • 확률계산의 곱셈법칙
    • P(A∩B) = P(A)P(B|A)
  • 독립, 통계적 독립, 확률적 독립:
    • 다음 세 조건중 하나라도 만족하면 독립
    • (1) P(A|B) = P(A)
    • (2) P(B|A) = P(B)
    • (3) P(A∩B) = P(A)P(B)

3.5 베이즈의 정리 (Bayes’ Theorem)

  • 사전확률 : 조건부 확률에서 사건이 발생하기 전 평가한 확률. ex) P(A), P(B)
  • 사후확률 : 조건부 확률에서 사건이 발생한 후 수정된 확률. ex) P(A|B)

  • 베이즈의 정리 :

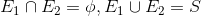
    bayes_condition

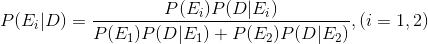
    bayes_thm

    m개의 상호배반인 사건들의 합집합이 표본공간과 같아지는 경우

    bayes_thm_m